卡瓦列里:卡瓦列里原理

大家好，今天小编关注到一个比较有意思的话题，就是关于卡瓦列里的问题，于是小编就整理了2个相关介绍卡瓦列里的解答，让我们一起看看吧。

米开朗琪罗是个什么样的人？

米开朗琪罗是一个意大利文艺复兴时期的雕塑家、画家、建筑师和诗人，他被视为人类历史上最伟大的艺术家之一。他的作品充满了对人类精神深度的探索和对美的追求。

他善于运用人体语言，通过细致入微的刻画和富有张力的构图，展现出人类的力量与美。他的作品不仅具有极高的艺术价值，也反映了文艺复兴时期的人文主义精神。

在牛顿之前，数学已经发展到什么程度了？

谢邀！按照一般的数学史分期理论，17世纪中叶之前，也就是大概在牛顿之前，数学的发展阶段属于古代数学，或初等数学的成熟期。所谓初等数学，主要有两个特征，其一是数与形相对独立，各自成为独立的科目，比如初等几何、三角学处理的对象以形状为主；而算术、初等代数则以数字为主。其二是在性质上属于常量数学，即所处理的对象相对比较具体，较少涉及变化的量。对初等数学做出重要贡献的包括埃及、巴比伦、古希腊、中国、印度和阿拉伯等古代文明。

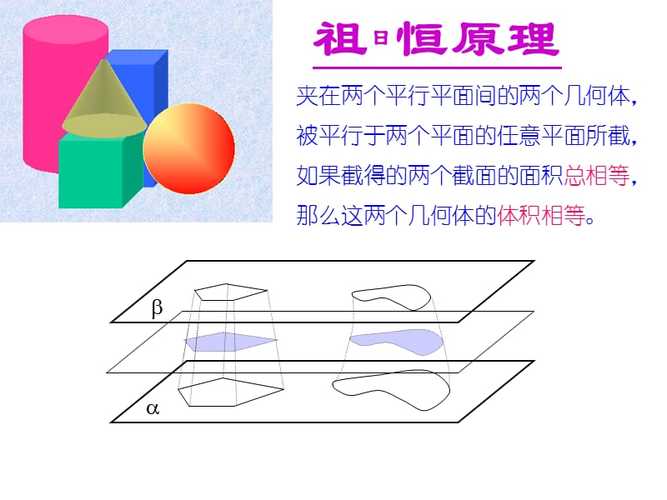
当然，如果严格以牛顿（与莱布尼兹）的微积分作为分水岭，则在他之前笛卡尔已经创立了解析几何，即1637年出版的《几何学》引入了直角坐标系，将数与形结合在一起，为变量数学和函数的发展奠定了基础。法国另一位数学家费马也为几何的代数化做出了重要贡献，他所遗留下来的费马大定理甚至成为历史上著名的数学难题，直到二十世纪末才得到解决。另外，天文学家开普勒也已具备了初步的微积分思想，他1615年发表《酒桶的新立体几何》一书，已经将酒桶视为若干薄圆片的积累，从而可以用这种方式求出酒桶的体积。伽利略的学生卡瓦列里则进一步建立了所谓“不可分原理”：线是由无穷多个点组成、面是由无穷多条线组成、体则是由无穷多个面组成。这也成为微积分的先声。

总之，到牛顿的年代，初等数学已经发展成熟，作为变量数学基础的解析几何、射影几何、高次代数方程都已经开始出现，甚至含有微积分思想的火花也频频展现，这些都使得微积分的建立成为水到渠成的事情。而微积分的建立，则使数学的发展进入到一个崭新的时期，即近代数学时期。

另外，值得一提的还有近代数学的一个重要分支概率论，在牛顿之前也已经开始奠基。其早期的主要贡献者是法国的帕斯卡和费马，荷兰的惠更斯等人，直到与牛顿差不多同时期的雅各布•伯努利（1654-1705）去世后由后人于1713年出版了他的遗著《猜度术》，概率论正式成为近代数学的一大分支。

一家之言，欢迎拍砖！

牛顿和莱布尼兹各自独立分明了微积分这种数学工具。

微积分可以说把数学，物理学，实际工程应用往前推进了一大步。

在此之前，数学只能对一些形状规则的特殊的几何进行相关几何量比如周长，面积等进行处理，稍微复杂一点 就无能为力。

可以这么说吧，自然界的运动，所有的运动，不管多么复杂，最终都可以用微分方程来表示。

在没有微积分这种思想和工具出现以前，稍微复杂一点的问题，是难以进行数学推导来得到他的微分方程的，自然也就没法研究他的变化规律。不用微积分，能够推导出来的都是一些比较特殊的情况。

所以，在牛顿之前，也就是在微积分出现之前，一切与微分方程有关的，一切与微积分手段有关的数学都还没很好的发展起来。

到此，以上就是小编对于卡瓦列里的问题就介绍到这了，希望介绍关于卡瓦列里的2点解答对大家有用。